Skip to main content
Contents Index Dark Mode Prev Up Next \(\usepackage{siunitx}
\newcommand{\lrp}[1]{\left(#1\right)}
\newcommand{\lrb}[1]{\left[#1\right]}
\newcommand{\lrbrace}[1]{\left\lbrace#1\right\rbrace}
\newcommand{\abs}[1]{\left|#1\right|}
\newcommand{\dint}{\displaystyle\int}
\newcommand{\defint}[2]{\dint^{#2}_{#1}}
\newcommand{\dlim}[2]{\displaystyle\lim_{#1\rightarrow #2}\,}
\newcommand{\dydx}{\dfrac{dy}{dx}}
\newcommand{\ddx}{\tfrac{d}{dx}}
\newcommand{\dddx}{\dfrac{d}{dx}}
\newcommand{\ifsol}[1]{\ifprintanswers{#1}\fi}
\newcommand{\Nat}{\mathbb{N}}
\newcommand{\Whole}{\mathbb{W}}
\newcommand{\Int}{\mathbb{Z}}
\newcommand{\Rat}{\mathbb{Q}}
\newcommand{\Real}{\mathbb{R}}
\newcommand{\Complex}{\mathbb{C}}
\DeclareMathOperator\arcsinh{arcsinh}
\DeclareMathOperator\arccosh{arccosh}
\DeclareMathOperator\arctanh{arctanh}
\newcommand{\lt}{<}
\newcommand{\gt}{>}
\newcommand{\amp}{&}
\definecolor{fillinmathshade}{gray}{0.9}
\newcommand{\fillinmath}[1]{\mathchoice{\colorbox{fillinmathshade}{$\displaystyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\textstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptscriptstyle\phantom{\,#1\,}$}}}
\newcommand{\sfrac}[2]{{#1}/{#2}}
\)
Section 12.5 The Differentiation Methods Tutor
The Differentiation Methods tutor is useful for showing each individual differentiation rule as a separate step when finding the derivative of a given function.
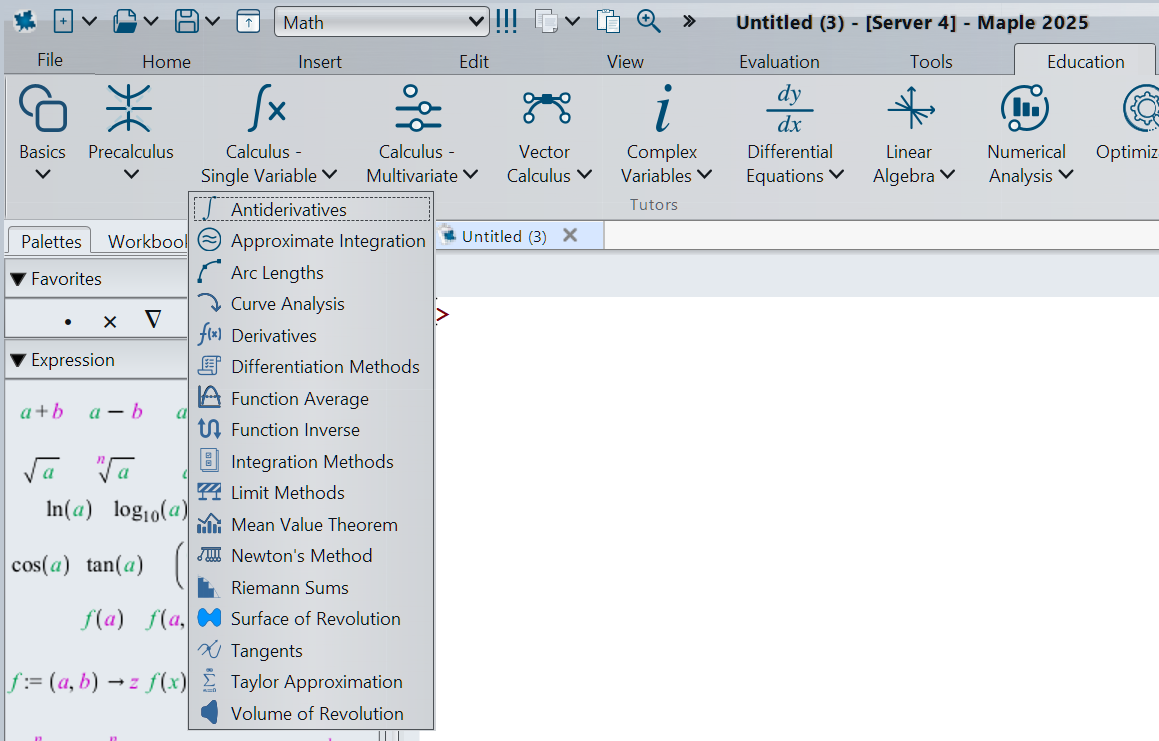
Figure 12.6. Opening up the Differentiation Methods tutor using menus.
Figure 12.7. Opening up the Differentiation Methods tutor using commands. The Student[Calculus1] package is required.
Example 12.8 . Differentiating \(x^2\cos(x)\) using the Product, Power, and Cosine Rules.
This example will use the Differentiation Methods tutor to show how various differentiation rules are applied to
\(x^2\cos(x)\text{.}\)
To begin, make sure that the function is typed in properly. You will not have access to the palettes toolbar in Maple, so you will need to type out commands such as
sqrt() for square roots. You must also include the symbol * for multiplication.
You will also need to ensure that the correct variable is specified. Then you can click Start to begin.
If you are unsure which rule should be applied, you can ask for a hint.
You can click on an appropriate differentiation rule to see the specific rule applied, along with the resulting expression. If a rule cannot be applied, then the tutor will provide additional hints.
With the product rule applied, you can continue on to use the power and cosine rules.
Example 12.9 . Differentiating \(\frac{\sin(x)}{x\tan(x)}\) by Simplifying and the Quotient Rule.
This example will show how to rewrite
\(\frac{\sin(x)}{x\tan(x)}\) in a simpler form in order to apply the quotient rule.
Once the function is typed in properly, make sure that the variable is properly set and click Start. In its original form, this expression requires both the product and quotient rules for differentiation. However, by rewriting
\begin{equation*}
\tan(x) = \dfrac{\sin(x)}{\cos(x)}\text{,}
\end{equation*}
the expression can be simplified to only require a quotient rule,
This simplification can be done by selecting the “Rewrite” rule and applying the given change.
After applying the simplification, the quotient rule can be applied directly.
Applying the remaining differentiation rules is left as an exercise for the reader.